Der Kreis und pi

1. Grundlegende Begriffe

1.1 Definition

Ein Kreis ist die Menge aller Punkte einer Ebene, die von einem festen Punkt dieser Ebene einen konstanten Abstand haben.

1.2 Bezeichnungen am Kreis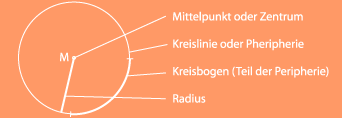

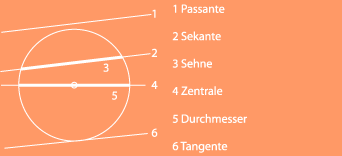
2. Berechnungen am Kreis

2.1 Umfang

Klicken Sie hier um ein Java-Applet zur Veranschaulichung zu starten.

Für die Länge des Umfangs U eines Kreises vom Durchmesser d kann man die Umfangslängen einbeschriebener und umbeschriebener regelmäßiger Vielecke als Schranken angeben, z. B. ist der Umfang U_i=3d des regelmäßigen einbeschriebenen Sechsecks eine untere und der Umfang U_a=2d<3,47d des regelmäßigen umbeschriebenen Sechsecks eine obere Schranke (siehe Abb.), so dass gilt 3,00d<U<3,47d.

Der Faktor, mit dem man d multiplizieren muss, um U zu erhalten, wird mit dem griechischen Buchstaben π [sprich pi] bezeichnet, U=π-d. Diese Konstante ist eine der wichtigsten und interessantesten mathematischen Konstanten; sie ist irrational und transzendent. Man kann sie um so genauer angeben, je größer man die Anzahl der Seiten der erwähnten Vielecke wählt.

Schon Archimedes hat seine Untersuchungen bis zum 96-Eck durchgeführt und dabei eine obere und eine untere Schranke für π ermittelt, die noch heute in der Praxis oft als hinreichend genaue Näherungswerte benutzt werden, vor allem die obere Schranke; er fand 3¹⁰/₇₁<π<3¹⁰/₇₀, d. h. 3,140 845 07<π<3,142 857 14.

π=3,14159 26535 89793 23846 26433 83279 50288 41971...

2.2 Flächeninhalt

2.2.1 Kreis

Auch der Fächeninhalt des Kreises ergibt sich als Grenzwert der Flächeninhalte der ihm ein- und umbeschriebenen regelmäßigen Vielecke mit der Zahl π als Proportionalitätsfaktor. Seine Fläche A=πr²=π(d/2)² ist dem Quadrat der Länge seines Radius proportional.

A=πr²=π(d/2)²

2.2.2 Kreisring

Als Differnz der Flächeninhalte zweier konzentrischer Kreise mit den Durchmessern d₁ und d₂ < d₁ erhält man A=(π/4)d₂²-(π/4)d₁²=(π/4)(d₂²-d₁²)=(π/4)(d₂+d₁)(d₂-d₁).

A=(π/4)(d₂+d₁)(d₂-d₁)

2.2.3 Kreissektor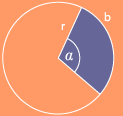

Da der Flächeninhalt A des Kreisausschnitts oder Kreissektors von der Größe des Zentriwinkels α abhängt und da zu α=360° der Inhalt der gesamten Kreisfläche πr² gehört, kann man die Proportion aufstellen A/πr²=α/360° A=(α/360°)-πr², für α in Grad. Wird die Winkelgröße α in Bogenmaß angegeben, so erhält man wegen der Gleicheit von (α/360°) für α in Grad und (α/2π) für α in rad die unten stehende Relation.

A=αr²/2 für α in rad

Die Länge des den Kreissektor begrenzenden Bogens b ergibt sich aus der Proportion b:α=2πr:360° für α in Grad bzw. b:α=2πr:2π für α in rad und kann in die Formel für den Flächeninhalt eingesetzt werden.

b=2πr-α/360°=απr/180° für α in Grad

A=πr²α/360°=br/2 für α in Grad

2.2.4 Kreissegment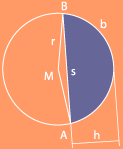

Die Fläche des Kreisabschnitts, des Kreissegments, gewinnt man als Differnz aus Flächeninhalt von Kreissektor und Dreieck AMB, A=br/2-s(r-h)/2, wobei s die Länge der Segmentsehne und h die Bögenhöhe bedeuten.

3. Satz des Thales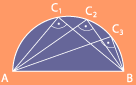

Der geometrische Ort der Scheitelpunkte C_i aller rechten Winkel, deren Schenkel durch zwei feste Punkte A und B gehen, ist der Kreis über der Strecke AB als Durchmesser.

4. Die Berechnung der Zahl pi

Die Arkustangensreihe kann zur Berechnung von π herangezogen werden. Sie lautet arctan x = x-x³/3+x⁵/5-x⁷/7-...
Bei dieser Reihe ist eine Angabe des Restgliedes R_n nach dem Taylorschen Satz nicht ohne weiteres möglich. Es ist zwar bekannt, dass die Funktion f(x)=arctan x Ableitungen beliebig hoher Ordnung hat; das Bildungsgesetz für höhere Ableitungen ist aber sehr kompliziert und kaum in einer allgemeinen Formel angebbar. Es bleibt daher nur der Weg, das Restglied aus einem allgemeinen Ansatz mit Hilfe des Mittelwertsatzes der Differentialrechnung zu gewinnen.

Durch Kombination mehrererArkustangensreihen für verschiedene Argumente gelangt man schließlich zu besonders bequemen Formeln, von denen einge angeführt werden, die zur Berechnung von π mit elektronischen Rechenautomaten verwendet werden können:

Die letzten beiden Formeln wurden 1961 der Berechnung von π auf 100.265 Dezimalstellen zugrunde gelegt. Zwei Machinen rechneten im Dualsystem, zur Kontrolle jede nach einer anderen Formel. Nach der Gaußschen Formel wurden 4 Stunden 22 Minuten gebraucht, nach der von Störmer 8 Stunden und 43 Minuten. Die Übertragung ins Dezimalsystem dauerte 42 Minuten; der Text umfasste 20 Druckseiten.

Zum Vergleich benötigt unser Beispiel-Java-Applet auf einem Rechner mit 800 Mhz ca. 20 Minuten. Man sollte jedoch beachten, dass hier die Berechnungen von einem recht langsamen Java-Interpreter ausgeführt werden, mit einem beispielsweise in C geschriebenen Programm würde sich der Rechenaufwand in wenigen Sekunden bewältigen lassen.

Beispiel-Java-Applet

Erstellt 2001-07-24 von Jens Borsdorf, Java-Applets von Andreas Tetzl.